
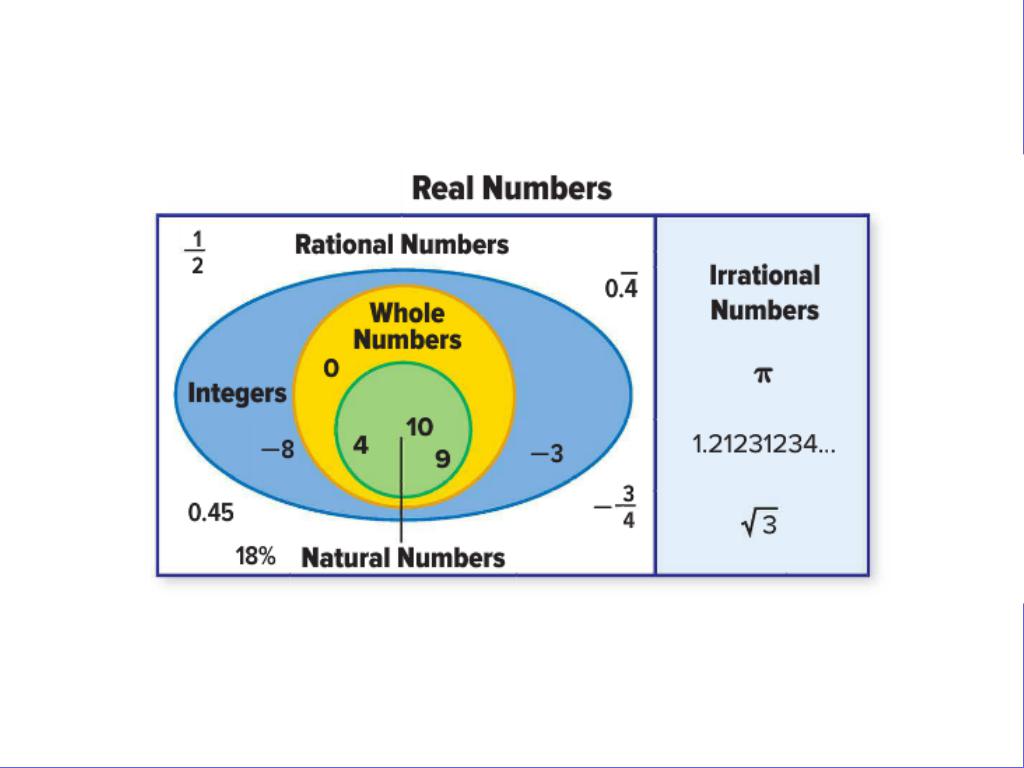
Likewise, ∞ is not a real number i and ∞ are therefore not in the set. The number i is imaginary, so it doesn't belong to the real numbers. Solution:If a number can be written as where a and b are integers, then that number is rational (i.e., it is in the set ). Practice Problem: Identify which of the following numbers belong to. Let's review these subsets of the real numbers:

Interested in learning more? Why not take an online Algebra course? The set of real numbers is composed entirely of rational and irrational numbers. An irrational number, on the other hand, is a non-repeating decimal with no termination. The symbol is often used for the set of rational numbers. Rational numbers thus include the integers as well as finite decimals and repeating decimals (such as 0.126126126.). A rational number is a number that can be equivalently expressed as a fraction, where a and b are both integers and b does not equal 0. The set of real numbers is divided into two fundamentally different types of numbers: rational numbers and irrational numbers. Obviously, we could add as many additional decimal places as we would like. Consider 1 and 2, for instance between these numbers are the values 1.1, 1.11, 1.111, 1.1111, and so on. There are an infinite number of fractional values between any two integers. In addition to the integers, the set of real numbers also includes fractional (or decimal) numbers. The set of integers is often referred to using the symbol. In addition to positive numbers, there are also negative numbers: if we include the negative values of each whole number in the set, we get the so-called integers.

If we add to this set the number 0, we get the whole numbers. These are formally called natural numbers, and the set of natural numbers is often denoted by the symbol. Let's look at some of the subsets of the real numbers, starting with the most basic.Ĭhildren first learn the "counting" numbers: 1, 2, 3, etc. Real numbers include a range of apparently different numbers: for example, numbers that have no decimals, numbers with a finite number of decimal places, and numbers with an infinite number of decimal places. The symbol is often used for the set of complex numbers.
(In fact, the real numbers are a subset of the complex numbers-any real number r can be written as r + 0 i, which is a complex representation.) Complex numbers are an important part of algebra, and they do have relevance to such things as solutions to polynomial equations.

Thus, 3 i, 2 + 5.4 i, and –π i are all complex numbers. A complex number is any number that includes i. Infinity (∞) is not a real number, although it is greater than any given real number also, is not a real number, since there is no number whose square is equal to –1.Īs a brief aside, let's define the imaginary number (so called because there is no equivalent "real number") using the letter i we can then create a new set of numbers called the complex numbers. Perhaps the best way to describe a real number is to identify numbers that are not real numbers. The particular representation, whether it be a fraction, a decimal, or another representation, does not matter. A real number can thus be 8, 4.357, –3/5, π,, or any other such number. The above illustration, of course, only shows a portion of the number line (it would be impossible to show the whole thing), and only certain numbers are labeled (–1, 0, 1, etc.).


 0 kommentar(er)
0 kommentar(er)
